Amélioration de la vitesse et de la qualité de génération d'image
Bienvenue dans la troisième partie de notre série sur la bibliothèque Diffusers. Dans cet article, nous explorerons des stratégies pour améliorer à la fois la vitesse d'inférence et la qualité des images générées. Ainsi, nous améliorerons les techniques discutées dans notre article précédent, mais aussi en utiliserons des nouvelles.
Remarque sur les bonnes pratiques
Avant d'entrer dans les détails techniques, il est important de noter que cet article ne suit pas toutes les bonnes pratiques généralement recommandées pour les projets de machine learning. En particulier, nous n'utilisons pas de versionnage de jeux de données, d'outils de suivi comme MLflow, ni de cadres d'optimisation d'hyperparamètres tels que Optuna. Ces pratiques sont essentielles pour un workflow ML robuste et seront abordées dans de futurs articles, mais pas immédiatement. L'objectif de ce tutoriel est de présenter un flux de travail simplifié, plus facile à suivre et à comprendre.
Analyse des données : l'étape cruciale#
L'analyse des données est une étape cruciale pour améliorer la qualité de la génération d'image.
Comprendre la distribution des données#
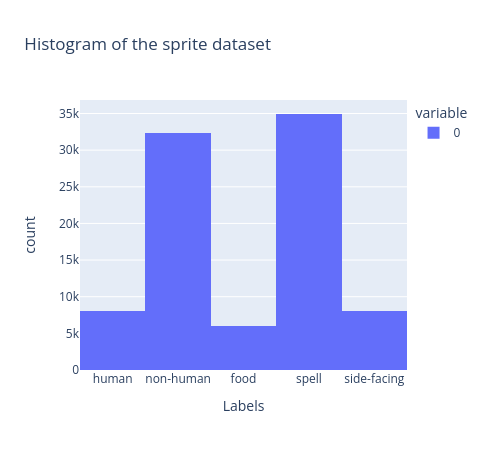
Commençons par examiner la distribution de notre jeu de données. Cela nous aidera à identifier tout déséquilibre ou anomalie dans les données.
Actuellement, notre jeu de données n'est pas équilibré. Le rééquilibrage des données améliorera la performance du modèle en renforçant sa capacité à généraliser et à produire des résultats plus précis. Nous pouvons le faire avec l'ajout suivant dans notre notebook d'entraînement :
dataset = SpritesDataset(
"./dlai_lib/sprites_1788_16x16.npy",
"./dlai_lib/sprite_labels_nc_1788_16x16.npy",
null_context=False
)
# Création d'un sampler pour compenser le déséquilibre du jeu de données
labels = dataset.slabels.argmax(axis=1)
u_labels, class_counts = np.unique(labels, return_counts=True)
class_weights = 1 - class_counts / class_counts.sum()
sample_weights = tuple(class_weights[label] for label in labels)
num_samples = ceil(len(labels)/batch_size) * batch_size # num_samples est un multiple de batch_size pour éviter de recompilation
dataset_sampler = WeightedRandomSampler(weights=sample_weights, num_samples=num_samples, replacement=True)
dataloader = DataLoader(
dataset, sampler=dataset_sampler, batch_size=batch_size, num_workers=1, pin_memory=True
)
Dans cette approche, nous calculons les poids pour chaque échantillon dans notre jeu de données et utilisons un échantillonneur de données aléatoire pour sélectionner les échantillons en fonction de ces poids. Ainsi, les échantillons des classes les moins représentées sont sélectionnés plus fréquemment que ceux des classes les plus fréquentes.
Malgré le fait que la classe non-humaine soit l'une des plus fréquentes dans notre jeu de données, le modèle peine à générer autre chose que des formes indistinctes, ce qui indique qu'il pourrait y avoir des problèmes sous-jacents avec les données elles-mêmes.
Analyse de la classe non-humaine#
Un défi majeur pour notre modèle est la classe non-humaine, qui inclut fréquemment des images mal définis. Pour illustrer ce problème, examinons d'abord les images non-humaines d'origine :
Comme on peut le voir, certains exemples sont de mauvaise qualité et ressemblent aux sorties non-humaines produites par notre modèle. Pour résoudre ce problème, nous allons étudier et développer une fonction pour détecter automatiquement de tels échantillons problématiques dans la base de données, car il n'est pas possible de revoir manuellement plus de 80 000 échantillons.
def detect_wrong_images(image: np.ndarray, number_of_white: int = 26) -> bool:
"""Fonction pour détecter si une image est incorrecte et doit être exclue de l'entraînement.
Paramètres
----------
image : np.ndarray
L'image en RGB avec une forme [largeur, hauteur, canal]
number_of_white : int, optionnel
Le nombre de pixels blancs qu'une image doit avoir pour être considérée comme valide, par défaut 26
Retourne
-------
bool
True si l'image est incorrecte pour la génération et False si elle est correcte.
"""
wrong_image = False
# Notez que le blanc est (255, 255, 255), donc la somme est 765
# Fond blanc donc un minimum de pixels doit être blanc
wrong_image |= np.sum(image.sum(axis=-1) == 765) < number_of_white
# Les 4 coins doivent être blancs
wrong_image |= image[0, 0].sum() != 765
wrong_image |= image[-1, 0].sum() != 765
wrong_image |= image[0, -1].sum() != 765
wrong_image |= image[-1, -1].sum() != 765
return wrong_image
L'objectif de cette fonction est simple : les bonnes images doivent avoir tous les coins blancs et une part significative des pixels doit être blancs, puisque nous nous attendons à des arrière-plans blancs. Bien que cette approche suffise pour un jeu de données relativement simple, des jeux de données réels nécessiteront des vérifications supplémentaires, telles que la netteté et des contraintes sur la palette de couleurs.
Si nous traçons quelques mauvais échantillons, nous obtenons ceci :
En utilisant cette approche, nous avons identifié et supprimé 30 000 échantillons problématiques de notre jeu de données, capturant efficacement les principaux problèmes de la classe non-humaine.
Et si nous montrons les 30 exemples non-humains de notre nouveau jeu de données, nous obtenons ceci :
L'application de cette fonction pour affiner notre jeu de données peut accélérer l'entraînement du modèle et améliorer significativement les résultats. Toutefois, vous constaterez peut-être que la qualité des images générées est encore insuffisante et que le processus de génération est trop lent. J'ai créé un jeu de données personnalisé pour permettre ce filtrage avec le paramètre clean_version=True.
Remarque : Pour une explication détaillée de ce processus, veuillez consulter le notebook dédié ici : https://github.com/vroger11/diffusers-tutorials/tree/main/tutorials/03-dataset_analysis.ipynb
Améliorations dans la conception du réseau#
On pense souvent qu'ajouter des couches et des paramètres supplémentaires améliorera le modèle. Bien que cela puisse être vrai dans certains cas, ce n'est pas la solution complète et cela conduit souvent à des modèles inefficaces. Dans les sous-sections suivantes, nous explorerons des techniques pour améliorer les résultats et la vitesse d'inférence.
Échauffement du réseau conditionnel#
Pour renforcer la concordance du résultat conditionné, nous utilisons une stratégie d'échauffement pour le réseau conditionnel. Mais, cela entraine un sur apprentissage de l'UNet sur la vérité terrain. Pour solutionner ce problème, après avoir gelé les paramètres du réseau conditionnel, nous appliquons un masquage aléatoire des étiquettes (contexte) en utilisant une distribution de Bernoulli. Cette approche stabilise le processus d'entraînement et aide à éviter que le UNet ne surapprenne au réseau conditionnel.
J'ai choisi une valeur d'échauffement arbitraire de 80 à des fins de démonstration dans ce tutoriel. Cela peut ne pas être la valeur optimale pour tous les scénarios. Dans des applications réelles, il est conseillé de surveiller les performances du modèle et d'ajuster l'étape d'échauffement en conséquence pour déterminer le meilleur moment pour geler le réseau conditionnel.
Ces ajustements sont mis en œuvre en incorporant les deux conditions suivantes dans notre boucle d'entraînement :
if epoch >= warmup:
warmup_done = True
# geler toutes les couches du réseau d'embeddings
for param in emb_net.parameters():
param.requires_grad = False
if warmup_done:
# masquage aléatoire des étiquettes (contexte)
context_mask = torch.bernoulli(torch.zeros(labels.shape[0]) + 0.95).to(unet.device)
labels = labels * context_mask.unsqueeze(-1)
Améliorations de l'architecture du réseau#
Améliorations de l'UNet#
L'ajout à la fois d'un bloc descendant et d'un bloc ascendant à l'architecture UNet s'est avéré efficace. Mes expériences ont montré que l'absence de ces blocs entraînait une baisse de la qualité des images générées.
Par conséquent, nous modifions notre UNet comme suit :
unet = UNet2DConditionModel(
encoder_hid_dim=class_emb_size,
sample_size=16,
in_channels=3,
out_channels=3,
layers_per_block=2,
block_out_channels=(64, 128, 256),
down_block_types=("DownBlock2D", "DownBlock2D", "CrossAttnDownBlock2D"), # Un bloc descendant supplémentaire
up_block_types=("CrossAttnUpBlock2D", "UpBlock2D", "UpBlock2D"), # Un bloc ascendant supplémentaire
)
Goulot d'étranglement du réseau conditionnel#
La mise en œuvre d'un goulot d'étranglement dans le réseau conditionnel impose une meilleure qualité des embeddings, ce qui améliore à son tour la performance globale.
Ainsi, notre réseau d'embeddings devient :
emb_net = CustomSequential(
nn.Linear(num_classes, class_emb_size//2), # goulot d'étranglement pour imposer une meilleure qualité des embeddings
nn.GELU(),
nn.Linear(class_emb_size//2, class_emb_size),
UnsqueezeLayer(dim=1),
)
Techniques de régularisation#
Les techniques de régularisation sont essentielles pour améliorer la généralisation du modèle final et éviter le surapprentissage :
Dropout#
Nous appliquons le dropout à la fois au UNet et au réseau d'embeddings pour réduire le surapprentissage et améliorer la robustesse du modèle.
Cela entraîne les modifications suivantes :
emb_net = CustomSequential(
nn.Linear(num_classes, class_emb_size//2),
nn.Dropout(0.1), # ajout du dropout pour régulariser le modèle
nn.GELU(),
nn.Linear(class_emb_size//2, class_emb_size),
UnsqueezeLayer(dim=1),
)
# Définir le modèle UNet
unet = UNet2DConditionModel(
encoder_hid_dim=class_emb_size,
sample_size=16,
in_channels=3,
out_channels=3,
layers_per_block=2,
block_out_channels=(64, 128, 256),
down_block_types=("DownBlock2D", "DownBlock2D", "CrossAttnDownBlock2D"),
up_block_types=("CrossAttnUpBlock2D", "UpBlock2D", "UpBlock2D"),
dropout=0.2, # ajout du dropout pour régulariser le modèle
)
Notez que nous évitons d'appliquer le Dropout à la sortie de notre réseau d'embeddings pour éviter des problèmes, tels que l'optimisation des valeurs d'embedding nulles dues au Dropout, qui pourraient affecter le mécanisme d'attention dans notre UNet.
Optimiseur AdamW#
Nous utilisons l'optimiseur AdamW, qui intègre la dégradation des poids. Cette technique favorise une meilleure régularisation en pénalisant les poids importants.
Pour configurer cela, nous devons modifier une importation :
from torch.optim import AdamW
De plus, il est nécessaire de changez la création de l'optimiseur en utilisant un weight_decay. Ici, j'ai choisi une valeur arbitraire qui fonctionne bien dans la plupart des cas mais qui mérite d'être sélectionnée plus soigneusement si vous avez les capacités de calcul :
optimizer = AdamW(chain(unet.parameters(), emb_net.parameters()), lr=lr, weight_decay=1e-4)
Ajustements du scheduler et de la fonction de perte#
DDIM vs. DDPM#
Le DDIM (Denoising Diffusion Implicit Models) présente plusieurs avantages par rapport au DDPM (Denoising Diffusion Probabilistic Models). Contrairement au DDPM, qui repose sur une chaîne de Markov pour débruiter séquentiellement les échantillons, le DDIM contourne le processus de Markov explicite en utilisant une approche non-Markovienne qui permet moins d'étapes de diffusion. Cela se traduit par un échantillonnage plus rapide et plus efficace, tout en maintenant ou en améliorant la qualité des images générées.
Le passage du DDPM au DDIM est simple ; nous devons simplement commencer par remplacer la création du scheduler de bruit :
# Utilisation du DDIMScheduler au lieu du DDPMScheduler
noise_scheduler = DDIMScheduler(num_train_timesteps=1000)
Comme l'API du DDIMScheduler est similaire à celle du DDPMScheduler, il n'est pas nécessaire de modifier le code autour du noise_scheduler. Cependant, nous devons réécrire notre pipeline, bien qu'il ressemble beaucoup à notre DDPMPipeline personnalisé.
class ConditionalDDIMPipeline(DDIMPipeline):
def __init__(
self, unet: UNet2DConditionModel, class_net: CustomSequential, scheduler: DDIMScheduler
) -> None:
super().__init__(unet=unet, scheduler=scheduler)
self.class_net = class_net
self.class_net.eval()
self.register_modules(class_net=class_net)
self.unet.eval()
@torch.no_grad()
def __call__(
self,
class_label: list[list[float]],
generator: Optional[Union[torch.Generator, List[torch.Generator]]] = None,
eta: float = 0.0,
num_inference_steps: int = 1000,
use_clipped_model_output: Optional[bool] = None,
output_type: Optional[str] = "pil",
return_dict: bool = True,
) -> Union[ImagePipelineOutput, Tuple]:
r"""
Fonction d'appel du pipeline pour la génération.
Arguments:
class_label (list[list[float]]):
Liste d'exemples one-hot. len(class_label) représente le nombre d'exemples à générer.
generator (`torch.Generator`, *optionnel*):
Un [`torch.Generator`](https://pytorch.org/docs/stable/generated/torch.Generator.html) pour rendre
la génération déterministe.
eta (`float`, *optionnel*, par défaut 0.0):
Correspond au paramètre eta (η) du papier [DDIM](https://arxiv.org/abs/2010.02502). Ne s'applique
qu'au [`~schedulers.DDIMScheduler`], et est ignoré dans les autres schedulers. Une valeur de `0`
correspond à DDIM et `1` correspond à DDPM.
num_inference_steps (`int`, *optionnel*, par défaut 1000):
Le nombre d'étapes de débruitage. Plus d'étapes de débruitage conduisent généralement à une image de
meilleure qualité, au détriment d'une inférence plus lente.
use_clipped_model_output (`bool`, *optionnel*, par défaut `None`):
Si `True` ou `False`, voir la documentation de [`DDIMScheduler.step`]. Si `None`, rien n'est passé
en aval au scheduler (utiliser `None` pour les schedulers qui ne prennent pas en charge cet argument).
output_type (`str`, *optionnel*, par défaut `"pil"`):
Le format de sortie de l'image générée. Choisissez entre `PIL.Image` ou `np.array`.
return_dict (`bool`, *optionnel*, par défaut `True`):
Si `True`, retourne un [`~pipelines.ImagePipelineOutput`] ; sinon, retourne un tuple simple.
Retourne:
[`~pipelines.ImagePipelineOutput`] ou `tuple`:
Si `return_dict` est `True`, un [`~pipelines.ImagePipelineOutput`] est retourné, sinon un tuple
est retourné dont le premier élément est une liste des images générées.
"""
batch_size = len(class_label)
# Échantillonnage du bruit gaussien pour débuter la boucle
if isinstance(self.unet.config.sample_size, int):
image_shape = (
batch_size,
self.unet.config.in_channels,
self.unet.config.sample_size,
self.unet.config.sample_size,
)
else:
image_shape = (batch_size, self.unet.config.in_channels, *self.unet.config.sample_size)
image = randn_tensor(image_shape, generator=generator, device=self._execution_device, dtype=self.unet.dtype)
# obtention du ground truth encodé
labels = torch.tensor(class_label, device=self.device)
with autocast(str(self.unet.device)):
enc_labels = self.class_net(labels)
# définition des valeurs de step
self.scheduler.set_timesteps(num_inference_steps)
for t in self.progress_bar(self.scheduler.timesteps):
# 1. prédire le bruit model_output
model_output = self.unet(image, t, enc_labels, class_labels=labels, return_dict=False)[
0
]
# 2. prédire la moyenne précédente de l'image x_t-1 et ajouter la variance en fonction de eta
# eta correspond à η dans l'article et doit être compris entre [0, 1]
# passer de x_t à x_t-1
image = self.scheduler.step(
model_output, t, image, eta=eta, use_clipped_model_output=use_clipped_model_output, generator=generator
).prev_sample
image = (image / 2 + 0.5).clamp(0, 1)
image = image.cpu().permute(0, 2, 3, 1).numpy()
if output_type == "pil":
image = self.numpy_to_pil(image)
if not return_dict:
return (image,)
return ImagePipelineOutput(images=image)
Nous avons modifié l'héritage et ajouté le paramètre eta pour assurer la compatibilité avec le DDPMScheduler. Avec ce scheduler, j'ai pu générer des échantillons de haute qualité en seulement 10 étapes, au lieu de 100, améliorant ainsi la vitesse d'inférence de notre modèle final de plus de 10 fois, car nous utilisons également une approche non-Markovienne.
Fonction de perte#
Nous passons de la perte L2 à la perte L1. La perte L1, ou erreur absolue moyenne (MAE), est moins sensible aux valeurs aberrantes par rapport à la perte L2 (erreur quadratique moyenne), ce qui la rend plus robuste et stable pendant l'entraînement. Cette robustesse aide à générer des images plus claires et plus cohérentes visuellement en réduisant l'influence des valeurs extrêmes et en assurant des mises à jour de gradients stables.
Dans notre code précédent, cela nécessite de modifier le calcul de la fonction de perte :
# Calculer la perte l1 au lieu de mse, elle offre une meilleure robustesse aux bruits
# ce qui est adapté aux modèles de diffusion, mais l'inconvénient est un entraînement plus lent
loss = torch.nn.functional.l1_loss(predicted_noise, noise)
Améliorations de l'entraînement#
Augmentation des époques#
Avec les modifications mentionnées, nous avons augmenté le nombre d'époques d'entraînement à 100. Cela garantit que le modèle soit bien entraîné et de mieux tirer parti de nos ajustements précédents.
Torch compile#
Pour accélérer l'entraînement, nous utilisions déjà la précision mixet. Néanmoin, nous pouvons faire mieux en utilisant torch.compile. Ceci nous permet de réduire de 30 % le temps d'entraînement. Notez que torch.compile n'a pas été utilisé pour le pipeline final, car nous avons nécessité un seul forward pour l'évaluation. Cependant, torch.compile offre des avantages significatifs en matière d'efficacité pour la mise en production des modèles.
Pour compiler nos réseaux, nous devons ajouter les lignes suivantes :
# compiler les réseaux pour des inférences plus rapides même pour l'entraînement
unet = torch.compile(unet, fullgraph=True)
emb_net = torch.compile(emb_net, fullgraph=True)
Pour ceux qui sont intéressés par des résultats encore plus rapides grâce à des techniques telles que la quantification et la distillation, je recommande de consulter le tutoriel de Hugging Face sur la diffusion rapide.
Résultat final#
Avant de présenter les résultats finaux, je tiens à fixer des attentes réalistes. Avec le jeu de données actuel (exempt d'exemples de mauvaise qualité), nous pouvons nous attendre à de bons résultats. Cependant, gardez à l'esprit que nous travaillons avec seulement cinq catégories dans notre ground truth, et les exemples au sein de chaque catégorie sont assez hétérogènes. En conséquence, bien que le modèle apprendra à distinguer les catégories, il ne capturera pas les "sous-catégories", limitant notre contrôle sur celles-ci. Ce manque d'homogénéité au sein des catégories permet au ground truth d'être plus facilement mélangé.
Regardons maintenant quelques échantillons de chaque classe :
Comme vous pouvez le voir, les images semblent assez soignées, mais de nombreux résultats générés sont presque identiques à certains exemples d'entraînement. Vous remarquerez peut-être des différences subtiles entre les originaux et les échantillons générés (notamment avec les petits détails sur les flammes). Pour mieux contrôler les sous-catégories, nous pourrions améliorer la vérité terrain en subdivisant les catégories existantes. Ce travail est laborieux s'il est effectué manuellement. Une approche plus efficace consiste à l'automatiser en appliquant des algorithmes comme k-means dans l'espace encodé de notre UNet sur les échantillons d'entraînement et à attribuer des noms aux catégories résultantes. Cela rendrait le mélange de catégories plus significatif et permettrait plus de flexibilité dans l'ajustement des embeddings.
Cependant, comme je dois fixer des limites pour ce tutoriel afin d'éviter qu'il ne devienne trop vaste, je considère cette partie hors du cadre.
J'espère que cet article aidera et/ou inspirera certains d'entre vous. Si vous avez des suggestions, n'hésitez pas à commenter ou à me contacter.
À bientôt, Vincent.